→ ada pembilang dan penyebut
Penyelesaian:
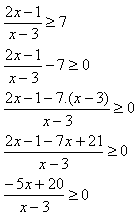
Harga nol pembilang: –5x + 20 = 0
–5x = –20 → x = 4
Harga nol penyebut: x – 3 = 0 → x = 3
Garis bilangan:
→ x = 3 digambar menggunakan titik putih karena merupakan harga nol untuk penyebut

Jadi penyelesaiannya: {x | 3 < x ≤ 4}
Contoh 2:

Harga nol pembilang: x – 2 = 0 atau x + 1 = 0
x = 2 atau x = –1
Harga nol penyebut: tidak ada, karena penyebut tidak dapat difaktorkan dan jika dihitung nilai diskriminannya:
D = b2 – 4.a.c = 12 – 4.1.1 = 1 – 4 = –3
Nilai D-nya negatif, sehingga persamaan tersebut tidak mempunyai akar real
(Catatan: jika nilai D-nya tidak negatif, gunakan rumus abc untuk mendapat harga nol-nya)
Garis bilangan:

Jadi penyelesaiannya: {x | x ≤ –1 atau x ≥ 2}
Penyelesaian:
- Ruas kanan dijadikan nol
- Samakan penyebut di ruas kiri
- Faktorkan pembilang dan penyebut (jika bisa)
- Cari nilai-nilai variabel yang menyebabkan pembilang dan penyebutnya sama dengan nol (harga nol untuk pembilang dan penyebut)
- Gambar garis bilangan yang memuat semua nilai yang didapatkan pada langkah 4
Apapun tanda pertidaksamaannya,
harga nol untuk penyebut selalu digambar dengan titik putih (penyebut
suatu pecahan tidak boleh sama dengan 0 agar pecahan tersebut mempunyai
nilai)
- Tentukan tanda (+) atau (–) pada masing-masing interval
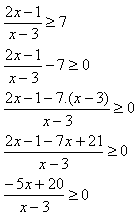
Harga nol pembilang: –5x + 20 = 0
–5x = –20 → x = 4
Harga nol penyebut: x – 3 = 0 → x = 3
Garis bilangan:
→ x = 3 digambar menggunakan titik putih karena merupakan harga nol untuk penyebut

Jadi penyelesaiannya: {x | 3 < x ≤ 4}
Contoh 2:

Harga nol pembilang: x – 2 = 0 atau x + 1 = 0
x = 2 atau x = –1
Harga nol penyebut: tidak ada, karena penyebut tidak dapat difaktorkan dan jika dihitung nilai diskriminannya:
D = b2 – 4.a.c = 12 – 4.1.1 = 1 – 4 = –3
Nilai D-nya negatif, sehingga persamaan tersebut tidak mempunyai akar real
(Catatan: jika nilai D-nya tidak negatif, gunakan rumus abc untuk mendapat harga nol-nya)
Garis bilangan:

Jadi penyelesaiannya: {x | x ≤ –1 atau x ≥ 2}
 RSS Feed
RSS Feed Twitter
Twitter 02.13
02.13
 Unknown
Unknown
 Posted in
Posted in
0 komentar:
Posting Komentar